IGCSE CORE SYLLABUS 2015

IGCSE Core Mathematics Syllabus 2015

Similar Triangles and Sine, Cosine, Tangent.

• Identify similar shapes

• Use Sin, Cos and Tan for acute angles

Similarity

Two shapes are Similar if the only difference is size (and possibly the need to turn or flip one around). Information on similar triangles.

See if you can figure out how tall a tree is without having to measure its height:

Right angled triangle ratios

Sine, Cosine and Tangent ratios

Remember:

Sohcahtoa

Soh...	Sine = Opposite / Hypotenuse
...cah...	Cosine = Adjacent / Hypotenuse
...toa	Tangent = Opposite / Adjacent

Click the image below for some extra exercises and further information:

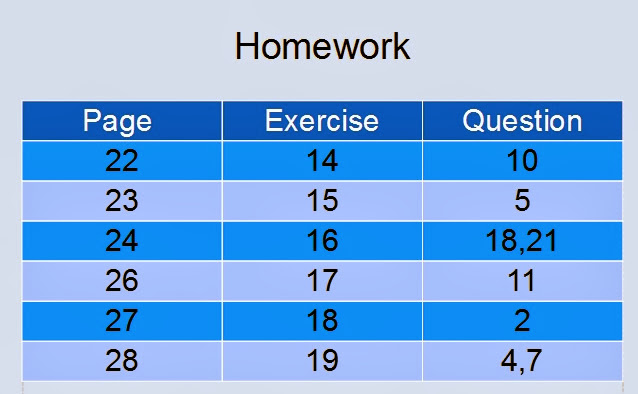
Homework:

P289 Ex1 Q. 6, 11, 13, 16, 17

P293 Ex 2 Q. 17-20

P293 Ex 3 Q. 4, 6, 7, 10, 11, 12

Form 9 Christmas Revision

Please review the work we have done in class this year and the material on this blog.
The following site will also be useful in your revision (note that some of the topics may not apply to IGCSE):

Make sure you complete the Christmas revision document which is available at the following link:
http://sdrv.ms/1c8SCuv.
(You can see the document at the end of this post). We will correct this in class at the start of term 2.

Finally please solve the revision problems and check the solutions for the sections listed below (these are from the following website):
http://www.newton.edu.pe/mathematics/Contents/ibrqs2/pag/igcse.htm)

• Algebra 1

• Area

• Area and Volume 

• Drawing Graphs

• Percentages 

• Linear Equations

Have a great Christmas and New Year!
Best wishes,
Mr. Healy

Loci

Objectives

• Locus from a fixed point

• Constructing a perpendicular bisector

• (to find the locus that is equidistant from two points)

• Locus from a line

• Constructing the bisector of an angle

• (to find the locus that is equidistant from two lines)

Locus from a fixed point

and the locus of all points at a fixed distance from a line.Watch the video here.

Constructing a Perpendicular Bisector

You can find the method by clicking on the image below:

Watch the video.

Constructing the perpendicular bisector helps you find the locus of points that are equidistant from two points.

Bisecting an angle

We use this method to find the locus of all points that are equidistant from two lines.

Some real world examples of loci

Watch a video of how loci apply in the real world.

 

Homework:

Bearings:

P191 Ex 19      Q 3, 4, 5

Loci:

P194   Ex 20    Q 4, 7, 9, 11

Quadrilaterals, Polygons, Bearing

Objectives:

- types of quadrilateral and polygons
- angles of polygons
- bearings

 

Types of Quadrilaterals

Polygons

Bearings

Homework:

Pg184 | Ex 12  | Q 3, 5, 7

Pg185 | Ex 13  | Q 3, 4, 6

Pg187 | Ex 14 | Q 3, 5

Pg188 | Ex 15 | Q 2

Pg190 | Ex 17 | Q 3, 4, 5 

Bring a compass next class!

Enlargements & Translations

Enlargement

Click the image above for more information, watch a video here.

Question P177 Ex 7 Q8

Translations

Reflection, Rotation and Enlargement

Objectives:

• Construct and reflect shapes in lines

• Rotate figures about a point

• Apply enlargements

Reflections:

Rotation

Enlargements

Homework

Pg 167    Ex 1    Q7

Pg 168    Ex 2    Q3

Pg 170    Ex 4    Q1

Scatter Plots, Excel and finding averages

Objectives:

• Line of best fit 

• Use Excel to display data

• Calculating the mean, median, mode and range for statistical data.

• Frequency polygons

 ___________________________________________

Scatter Plots

See an Excel tutorial on how to draw a scatter plot and line of best fit

 

Review of mean, median and mode:

 

Remember that very large or very small figures in a list of data can affect the mean and the range.

The median and the mode are less affected.

Frequency Polygons

Just as 'averages' can be misleading, look at this link to see how graphs of statistical data can be misleading.

Homework

(P143      Ex 8    Q5)

(P153      Ex 10  Q3, Q11)

P158      Ex 11  Q3

P160       Ex4A  Q6

P164/165   Ex 4B  Q7

Handling Data

Objectives:

Construct and interpret:

• Pictograms, 

• Pie charts, 

• Tally charts and Frequency diagrams,

• Grouping data

Conversion Graphs

 

Pictograms

Pie Charts

Bar Charts & Frequency Diagrams

Conversion Graphs   [PDF]

Homework

Pg 133     Ex 4     Q2

Pg 136     Ex5      Q3

Pg 137     Ex6      Q2

Graphs, gradients and lines

Objectives:

• Drawing curved graphs

• Calculate the gradient and intercepts of a line

• Solving equations graphically

 

Straight line graphs: 

This link shows how a line changes as you change the values.

Curved Graphs: 

Have a look here to see how changing the constants in an equation changes the shape of the graph.

Homework:

Page 56    Ex 11  Q: 5

Page 57    Ex 12  Q: 1 i,j; Q2

Page 59    Ex 14  Q: 9, 10, 15, 23

Page 62    Ex 16  Q: 4

Equations

Objectives:

-Solving Equations: Variable on both sides; fractions; geometrical;

-Drawing linear graphs

 Solving Equations:

Review here

Some problems and how to solve them. 

Homework:

Page 48 Ex 4 Q: 16, 22,28

Page 48 Ex 5 Q: 13, 16, 19

Page 49 Ex 6 Q: 21, 26, 31

Page 49 Ex 7 Q: 5

Page 50 Ex 8 Q: 5, 12

Page 51 Ex 9 Q: 5, 7, 11

Page 54 Ex 10 Q:11

Angles, Lines and Polygons

Objectives:
To know that the angles of a triangle add up to 180°
Angle properties of parallel lines
To know that the sum of the interior and exterior angles of quadrilateral add up to 360°
Tangents and triangles in a semi-circle

The angles of a triangle add up to 180°

Angle properties of parallel lines

 

Interior Angles of Polygons

An Interior Angle is an angle inside a shape.

Triangles

The Interior Angles of a Triangle add up to 180°

90° + 60° + 30° = 180°	80° + 70° + 30° = 180°
It works for this triangle!	Let's tilt a line by 10° ... It still works, because one angle went up by 10°, but the other went down by 10°

Quadrilaterals (Squares, etc)

(A Quadrilateral has 4 straight sides)

90° + 90° + 90° + 90° = 360°	80° + 100° + 90° + 90° = 360°
A Square adds up to 360°	Let's tilt a line by 10° ... still adds up to 360°!
The Interior Angles of a Quadrilateral add up to 360°

Because there are Two Triangles in a Square

The interior angles in this triangle add up to 180° (90°+45°+45°=180°)

... and for this square they add up to 360° ... because the square can be made from two triangles!

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

Exterior angles of a polygon add up to 360

 

Names of polygons

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

The angle between the tangent and radius is 90°

A tangent to a circle is a line which just touches the circle.

Remember:
A tangent is always at right angles to the radius where it touches the circle.

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

The triangle drawn on the diameter of a circle is always a right angles triangle

We could also rotate the shape around 180° to make a rectangle! It is a rectangle, because all sides are parallel, and both diagonals are equal. And so its internal angles are all right angles (90°).

Volumes, angles and triangles

28/10/2013

Objectives:

• Calculate volumes of prisms and cuboids

• Determine volume and surface area of cylinders

• Constructing triangles given sides and angles

• What are 'nets'?

• Angle Facts

Cuboids

A cuboid is a box-shaped object.

Prisms

A prism has flat sides and the same cross section all along its length.

Cylinders

Using a protractor

Nets

A 'net' is the shape you get when you cut along the edges of a three dimensional object and lay it out flat.

Other objects:

Angle Facts

>>>>>>>>60 second challenge<<<<<<<<<<<

Summarise in your copybook what we have learned today.

Circles & Areas

Sunday 27 October 2013

Objectives:

• Review of circle terms, circumference and area.
• Calculate the areas of more complicated shapes
• Areas of rectangles and triangles
• Definition and areas of parallelograms and trapeziums

Circles:

Copy the diagram and label each of [AB], [CD], [EF], [GH]

 Answer is here.

Copy the picture below, label the green and blue sections:

Answer is here.

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

Circle: Area and circumference

Area of a rectangle:

 

Area of a triangle:

More: Area of a triangle inside a rectangle

Area of a trapezium:

Note: this shape is also known as a trapezoid.

Area of a parallelogram:

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

Bring your protractors tomorrow please! 

 

>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>